Artigo de um AMIGO e IRMÃO

Bagé, 30.07.2021

O Coronel de Engenharia Higino Veiga Macedo, meu Caro AMIGO e MENTOR (com letras maiúsculas mesmo), enviou-me outro texto de sua autoria que faço questão de compartilhar com os leitores.

Carta ao Felipe – Geometria e Potência de Números

Por Higino Veiga Macedo, João Pessoa, PB, 26.07.2020

Felipe (*):

Quero escrever sobre algo que não vi em livros sobre aritmética ([1]) e geometria ([2]). Estou todo enrolado como começar. Gostaria de começar pelos gregos antigos, mas tenho medo de ter entendido errado e passar algo errado. Mas vou procurar me conter sobre eles. Vou arriscar. Vou seguir Descarte: se não sei começar, começo qualquer coisa e vou me corrigindo no caminho.

A geometria se fundamenta em Euclides (de Alexandria). Não se sabe ao certo seu local de nascimento e morte, mas apenas que viveu durante o reinado de Ptolomeu Sóter (Ptolomeu I – entre 323 a.C. e 283 a.C. Egito). Esses “Ptolomeus” foram descendentes de um General de Alexandre. Euclides era pitagórico.

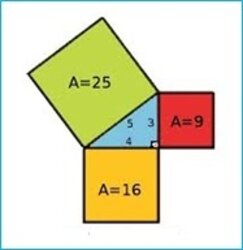
Lendo a obra de Bertrand Russell entendi que, no meio do caminho, Pitágoras sente a necessidade de juntar a aritmética com a geometria. A coisa passa pelo seu teorema. Entretanto, há quem diga ([3]) que o teorema na verdade não é dele.

O conceito era de conhecimento mais antigo (indus, egípcios, babilônios). Há a máxima atribuída a ele: “tudo é número”. Pelo que entendi até agora, a junção da aritmética com a geometria deu origem à matemática ([4]). Pitágoras então é o grande mentor da junção da geometria e a aritmética com seu clássico, simples e desafiante teorema.

 Quando iniciei o estudo de Geometria Descritiva (1° ano científico), o professor, um suíço de nome Demichelis (deve ser esta a grafia), deu um susto na sala. Disse que era uma matéria muito fácil. Tudo começava pelo PONTO, passava pela RETA, seguia pelo PLANO e chegava ao SÓLIDO. A RETA nada mais era que UM PONTO se deslocando numa direção; poderia ser ainda INFINITOS PONTOS um ao lado do outro; infinitas retas construía o PLANO; infinitos planos construía o SÓLIDO. Apenas, e somente apenas, um detalhe: o PONTO NÃO EXISTE. Qualquer que seja o instrumento que se use para aumentar a visão do ponto, ele será uma circunferência, uma área. Mas, adimensional (sem medidas). Vai ao infinito.

Aí vêm as brigas de filósofos gregos: uns diziam que o infinito existe, como o ponto; outros diziam que tudo tinha uma finitude (o infinito não existe): a menor parte que se obtinha era o átomo (indivisível, em grego); outros provavam que havia o infinito: Paradoxo de Zenão – a corrida de Aquiles contra a tartaruga (que tenho certeza seria um jabuti e não tartaruga que é da água).

E para complicar mais, quando se lança o ponto ou a reta ou o plano, na dita geometria plana, e ou os sólidos, na geometria espacial, o papel no qual se desenha é um plano. Mas o papel plano, que tem comprimento e largura, tem uma espessura sempre desprezível. A espessura é do papel, não do desenho. O que forçamos o cérebro para ler a terceira dimensão (sólido, espaço), na verdade é desenhado num plano. O coitado do cérebro que se vira para ver a terceira dimensão, a profundidade, a perspectiva.

Admiro os clássicos exatamente por eles terem escrito isso tudo sem régua, sem esquadro, sem medidas-padrão, sem compasso, sem lápis, sem papel e sem borracha. Desconfia-se que desenhavam na areia. E no cérebro. Bom, tudo isso para dizer que a ciência, hoje, é o que é depois que filósofos juntaram geometria e aritmética, inventando a MATEMÁTICA: Pitágoras, Platão, Euclides, Descarte, Gaspard Mong, Newton, Leibniz, Einstein e até Stephen Hawking. O que eu proponho é entender a relação entre a potenciação dos números e as figuras geométricas euclidianas (sem endoidar em decorar os princípios e teoremas e axiomas). Imagino que ficará mais fácil entender as raízes, logaritmos e outras unidades muito grandes e ou muito pequenas.

1) A POTENCIAÇÃO

Particularmente acho que, sem entender as regras básicas da potenciação, muito dificilmente se entenderá álgebra, logaritmo, trigonometria, enfim, a junção maior da geometria e matemática formando a geometria analítica. Sempre achei engraçado: as equações são mais letras que números. Mas “tudo é número”. Aqui, é melhor usar o número três porque, a partir dele, se chega a qualquer outro. Portanto, será BASE 3. Economiza-se trabalho braçal. Para o entendimento basta chegar ao 3⁷. Para facilitar, uma tabela:

(*) cada item será uma consideração.

2) A GEOMETRIA

A geometria passará pela reta, pelo plano e pelo sólido.

A medida será tratada como uma unidade de medida ou u;

3) A COMPOSIÇÃO

É a tentativa de, ao ver um, ver também o outro: aritmética e geometria.

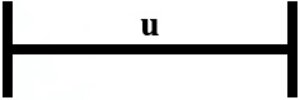
1ª CONSIDERAÇÃO ‒ (Figura 01)

Geometria ‒ Uma reta (semirreta), com VALOR padrão admitido como UNIDADE PADRÃO; Estabelece-se valor do comprimento (maior medida) e ou largura (segunda medida que estabelece o plano). Uma ou outra serão semirretas e se cruzam.

Aritmética ‒ uma unidade (1u) como medida: VALOR padrão admitido como UNIDADE PADRÃO.

2ª CONSIDERAÇÃO – (Figura 02)

Geometria ‒ Semirreta (reta) que pode ser comprimento ou largura com valor de UNIDADE PADRÃO variável.

Aritmética – Neste exemplo, toma-se três unidades-padrão = 3u como medida.

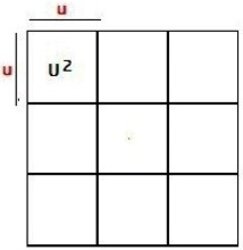
3ª CONSIDERAÇÃO – (Figura 03)

Geometria ‒ Plano ‒ Na geometria passa-se da Reta ao Plano. Sempre contido numa SUPERFÍCIE ([1]), Tem-se a Área. A área é L x L ou L². Mas o Plano não existe, porque não existe a reta e não existe o ponto. É um ente intuído, imaginado, concebido. O Plano, a superfície, sempre contido num ESPAÇO.

Aritmética ‒ Na aritmética se entra na Potenciação. Este plano é um quadrado de 3 medidas de lado (3u) – 3X3. Deixou de ser uma medida só. Tem duas: comprimento e largura, que no caso são iguais. Portanto, 3x3 é também uma Figura geométrica quadrada. Sua área, a superfície que ocupa, é de 9 unidades quadradas, ou seja, 3x3 = 3² = 9. Não tem altura.

4 ª CONSIDERAÇÃO ‒ (Figura 04)

Geometria - Na geometria se entra pelo sólido (prisma). É uma área (superfície) com uma unidade (1u) em terceira dimensão o que estabelece volume (espaço). Aqui entra uma consideração que sei, mas não me lembro da fundamentação. É o conceito de “o infinito estar contido no finito”. Entre dois números inteiros, há as subdivisões que variam do zero ao mais infinito. Ou seja: em [n e n+1] = n/∞. Como se viu, o plano não existe. Para chegar ao valor da unidade “u” é como se fossem colados, plano sobre plano, infinitos planos.

Aritmética -

Portanto, se vê 1 X 3 X 3 pela Figura. É como se levantasse dois planos, na média de “1u”. Considerando as unidades, tem-se: 1 x 3 x 3 = 9 unidades; se considerar o plano, serão nove unidades quadradas; se considerar a unidade, da geometria espacial, se terá 9 unidades de volume.

5ª CONSIDERAÇÃO ‒ (Figura 05)

Geometria ‒ Também é um sólido. Este valor é o valor da área do quadrado com duas (2u) unidades na terceira dimensão. Portanto também em um prisma. É o dobro da consideração 04.

Aritmética ‒ Na potenciação tem-se 2 X 3 X 3 ou 2 X 3². Ou seja, têm-se o quadrado de três unidades no plano e duas unidades (2u) na terceira dimensão; se considerar a unidade, da geometria espacial, se terá 2 x 9 unidades de volume ou se tem 18 unidades de volume. Vale a consideração de infinitos planos colados até o valor de “2u”.

6ª CONSIDERAÇÃO – (Figura 06)

Geometria – A Figura (imagem) geométrica espacial é um CUBO ou hexaedro para os euclidianos. Trata de volume (espaço). E a representação aritmética também o chama cubo - o volume é L³ ou seja LxLxL; É prisma, hexaedro, com nome próprio – CUBO;

 Aritmética – Trata de 3³. É um plano, com a mesma medida na terceira dimensão. Assim têm-se três medidas iguais, o que cria a imagem do cubo; as medidas, para o cálculo do volume do cubo, no caso de três unidade é: 3x3x3 ou 3³. Considerando a unidade, tem-se então 27 unidades de volume. Agora a medida será igual a uma medida de volume: U = u³. Penso que se pode falar não mais de “unidade de volume”, mas sim da real unidade, ou seja, unidade cúbica: m³; pol³; pés³. 

7ª CONSIDERAÇÃO ‒ (Figura 07)

Geometria ‒ As considerações seguintes serão em função do CUBO. Claro que as potências viajam por diferentes bases e expoentes, mas a Figura geométrica fica retida no cubo. Na verdade, tais cubos formariam uma semirreta, unidos face a face, lado a lado como se infinitos pontos fossem. Como lá na reta. Teria a representação de uma semirreta de 3 unidades de cubos.

Aritmética – Este item trata então de 3⁴; Mas o que é esta potência? Sua representação é 3 X 3 X 3 X 3 ou 3⁴ ou ainda 3x 3³. Isto é, têm-se três grupos de três ao cubo. Em unidades cúbicas é igual a. 81. (Figura 07).

8ª CONSIDERAÇÃO – (Fig 08)

Geometria – Agora tudo se volta para o número de cubos, formando desenho geométrico correspondendo a valores potencializados que aqui a base é 3 e os expoentes variados. Na Figura geométrica se terá “um quadrado formado de três cubos” de lado. Pela dificuldade de desenho, ficará representado, mas deveria ser cubos face a face, lado a lado.

Aritmética – Aqui se tem 3⁵ (3x3) x (3x3x3) isto é, pode-se ler um quadrado de cubos. A imagem aritmética fica assim: 3² x 3³ O valor unitário, cúbicos, será: 3x3x3x3x3 = 243. Ou ainda 9 cubos com 27 unidades cúbicas, igual a 243 unidades cúbicas, unidades de volume.

9ª CONSIDERAÇÃO – (Figura 09)

Geometria ‒ A Figura fica difícil de ser reproduzida sem a ajuda de algo como um programa de desenho arquitetônico (tipo CAD). Nessa nona consideração, tem-se um cubo formado por cubos. Cubo de cubo. Para tal a “Figura 06” será repetida com a consideração de que cada unidade cúbica represente um cubo de três unidades.

Aritmética ‒ Nessa nona consideração que é ‒ 3⁶, a Figura aritmética é 3³ x 3³. Ou (3x3x3) x (3x3x3); ou (3³)². O valor em unidades cúbicas será 3⁶ = 729. 

10ª CONSIDERAÇÃO – (Figura 10)

Geometria – A dificuldade da representação também é alta. Mas com a mesma boa vontade da nona consideração fica mais fácil partindo do ponto em que a leitura aritmética é para três cubos formados por cubos. Então serão três cubos de cubos. Com o mesmo critério, repete-se a Figura 07 considerando que cada unidade seja um cubo de 3;

 Aritmética – A consideração aqui é o número 3 elevado à 7ª potência ou 3⁷. A leitura é 3 X 3³ X 3³; O valor em unidades cúbicas é 3⁷ = 2.187. O que chama a atenção é o valor em unidades. Por isso serem os crescimentos rápidos chamados de exponencial, uma vez que os expoentes aceleram os valores.

4. Considerações Finais

Se alimentar a curiosidade a coisa tende ao infinito, infinito o qual Sócrates queria que ficasse no átomo (indivisível) e que Zenon defendeu colocando Aquiles para competir com um jabuti.

A geometria plana (superfície) acompanha a espacial sendo claro o fundamento de qualquer tipo de geometria mesmo depois de a geometria analítica incorporar as curvas, “a posteriori”. Felipe, penso eu que, depois dessa carta, ao trabalhar com números apenas, você se lembre de que junto tem uma Figura, seja por elevar ao quadrado ou ao cubo. Até mesmo as potências maiores. Aqui se foi até à sétima potência.

NAMASTE, Felipe!!!

PS: ‒ A loucura dos teoremas de Euclides: em 1 ponto passam ∞ retas; agora, em dois pontos, só passa 1 única reta; em 1 reta passam ∞ planos, mas, em 2 retas, só passa 1 único plano.

(*) FELIPE – Felipe Taumaturgo Macedo de Sousa, filho de Karina T.M de Sousa e Manoel de Sousa Junior, meu neto. Nesse instante tem 9 anos de idade, cursa a 6ª série no Colégio Militar de Brasília. O presente texto é uma carta, de tantas outras que deixarei a ele, para serem lidas e entendidas quando adulto. Hoje Felipe é habilitado, com fluência escrita e falada, em inglês e habilitado em espanhol.

Solicito Publicação

(*) Hiram Reis e Silva é Canoeiro, Coronel de Engenharia, Analista de Sistemas, Professor, Palestrante, Historiador, Escritor e Colunista;

·     Campeão do II Circuito de Canoagem do Mato Grosso do Sul (1989)

·     Ex-Professor do Colégio Militar de Porto Alegre (CMPA) (2000 a 2012);

·     Ex-Pesquisador do Departamento de Educação e Cultura do Exército (DECEx);

·     Ex-Presidente do Instituto dos Docentes do Magistério Militar – RS (IDMM – RS);

·     Ex-Membro do 4° Grupamento de Engenharia do Comando Militar do Sul (CMS)

·     Presidente da Sociedade de Amigos da Amazônia Brasileira (SAMBRAS);

·     Membro da Academia de História Militar Terrestre do Brasil – RS (AHIMTB – RS);

·     Membro do Instituto de História e Tradições do Rio Grande do Sul (IHTRGS – RS);

·     Membro da Academia de Letras do Estado de Rondônia (ACLER – RO)

·     Membro da Academia Vilhenense de Letras (AVL – RO);

·     Comendador da Academia Maçônica de Letras do Rio Grande do Sul (AMLERS)

·     Colaborador Emérito da Associação dos Diplomados da Escola Superior de Guerra (ADESG).

·     Colaborador Emérito da Liga de Defesa Nacional (LDN).

E-mail: hiramrsilva@gmail.com